Codenames Clue Generator

What is Codenames?

Codenames is a word guessing game. Two teams compete to guess which words belong to their team from a 5x5 grid of words. On each game, the team selects a spymaster to provide clues to their teammates. Each clue consists of a single word followed by a number indicating how many words are associated with the clue.

For example, the spymaster may come up with the clue "pet 3" to refer to the three words dog, cat, and fish.

I have always enjoyed playing this game, but it can be difficult to come up with clues on my own. I decided to develop an algorithm to help me.

Overview of the approach

For my first pass at this, I wanted to see if I could successfully cluster a list of words by their semantic similarity, and then find a clue word that is "closest" to the cluster. To determine word-word similarity, Using the pretrained GloVe word embeddings for each word, we can define "similarity" by the angle between the word vector representations. With a simple way to determine word-word similarity, I used Scikit-learn's hierarchical clustering library to group the words into overlapping clusters. I selected the top clusters, and found the top clue words related to each cluster by finding the closest nouns, verbs or adjectives from the top 40K words from Google n-grams (with some curation by me).

Grouping the words

In order to come up with a set of clues for subsets of the words, we need to identify subsets based on their relatedness. There are many ways to group a collection of words, such as by their semantic similarity (e.g. dog-cat are closer than dog-cup), their relation to one another in a story (the man uses a computer to play music), or hierarchical relationships (father-son would be closer than grandfather-son), just to name a few. For simplicity, I am using the semantic relationship between words as represented by the distance between the GloVe vectors.

GloVe word vectors

GloVe (Global Vectors for Word Representation) are vectors representing a word in high-dimensional space (often called word embeddings). They can be used to compare words by their semantic similarity. By comparing the cosine of the angle between the word vectors (cosine similarity), we can determine how related two words are. For example:

cosine similarity (smaller is better):
dist(dog,    cat)    = 0.318
dist(dog,    tree)   = 0.713
dist(flower, tree)   = 0.539
dist(dog,    flower) = 0.829

Clustering the words

There are many approaches to cluster a group of data points, or word vectors, based on their distance. We could use k-means to specify a desired number of clusters, and partition the points into that number of clusters. I considered this approach, but decided that we do not know a priori how many groups the words naturally fall into, making this method unsuitable for our problem. Instead, I decided to cluster the words hierarchically based on their semantic overlap. To accomplish this, I used Scikit-learn's hierarchical clustering algorithm.

To use this algorithm, we first must construct a similarity matrix of size len(words) x len(words) with the matrix populated by the distance between each word.

The distance is calculated by cosine similarity. The cosine of the angle between two vectors, a and a, can be calculated as:

cos(a, b) = 1 - (a • b) / (|a| * |b|)

The magnitude of a vector is its distance from the origin. This can be determined using the distance formula, where the second point is the origin:

|a| = sqrt(sum((b)^2))

This can be written in python using numpy functions as:

cos_ab = 1 - dot(a, b) / (sqrt(sum(a**2) * sum(b**2)))

If we want to calculate the dot product between two arrays of vectors (e.g. two matrices), we can speed up this computation by vectorizing the calculation.

The dot product is the sum of the element-wise multiplied values between two vectors. In matrix form, where each row corresponds to a vector, we can use matrix multiplication to perform the same function in one operation. Given two matrices, A and B, we can convert,

similarity_matrix = zeros((len(A), len(B)))
for i in range(len(A)):
    for j in range(len(B)):
        similarity_matrix[i,j] = 1 - dot(a[i], b[j]) / (sqrt(sum(a[i]**2) * sum(b[j]**2)))

to the vectorized form:

similarity_matrix = A @ B.T
A_normed = expand_dims(sqrt(sum(A**2, axis=1)), 0)
B_normed = expand_dims(sqrt(sum(B**2, axis=1)), 1)
similarity_matrix = 1 - similarity_matrix / (A_normed * B_normed)

Given the following list of words and their vectors,

words = ['cat',  'dog',    'house', 
         'tree', 'flower', 'fish']

the calculation gives us the following similarity matrix:

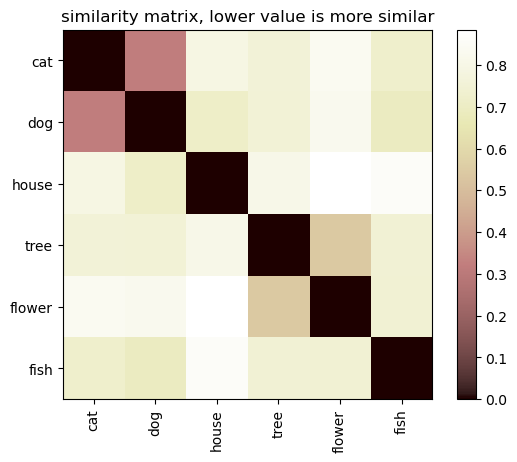
With this in place, we call the function

hierarchy.linkage(similarity_matrix, 'average')

which returns a condensed representation of the cluster hierarchy (called a linkage). We choose the 'average' linkage type as it works best for non-Euclidean distance metrics, which includes cosine distance between words.

We can visualize the word hierarchy with scikit-learn's dendrogram function.

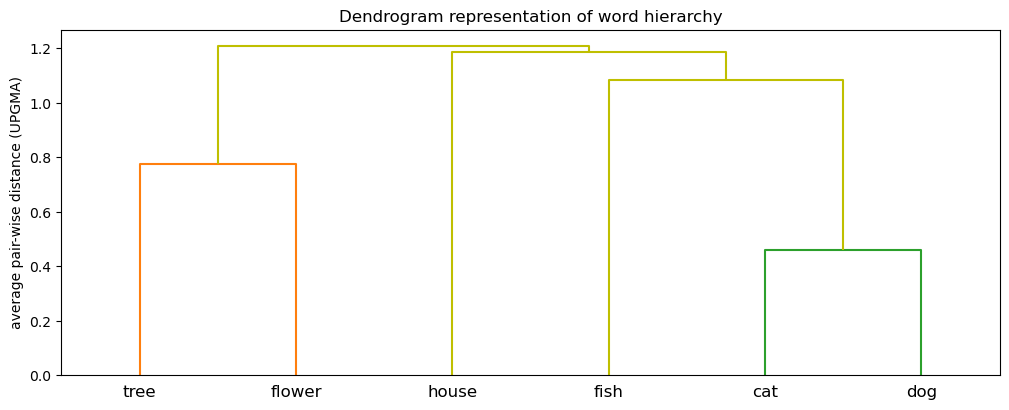
The cluster representation returned by the linkage function is compressed, and some work needs to be done to extract the word groups from it.

[[0,  1,  0.45871543,  2],
 [3,  4,  0.77507536,  2],
 [5,  6,  1.08339834,  3],
 [2,  8,  1.1873115,   4],
 [7,  9,  1.20697873,  6]]

Each row identifies a pair of words, or clusters, the distance between the pair, and the number of elements in that cluster. Because we are using the average linkage method, the distance between clusters is the average of all distances between pairs of objects in each cluster (see UPGMA). The meaning of this distance will be different depending on the linkage method you choose.

The rows are sorted by distance, in ascending order. The values for the pairs start as the index of that word in the words array. Any values larger than len(words)-1 specify the ID for a cluster. We iterate over the rows and construct a tree, creating leaf nodes for any IDs in the words array, and intermediate nodes for cluster IDs. We retrieve all of the elements of a given cluster through a depth-first traversal of the tree starting at the cluster's node.

Finding the best clue from the cluster

Once we have the words grouped into clusters, we need to find a good clue for the words in that cluster. To recap, a clue in the Codenames game consists of a single word and the number of words in the group that the clue relates to. Additionally, the clue cannot simply be a word on the board or some variation of that (e.g. cats for the word cat, or running for the word run). The general approach is to find a clue word that is closest to all of the words in the given word cluster.

To begin with, we need a list of potential candidate words to use as clues. I used the list of the most common 10,000 English words (without swears) scraped from Google Ngrams from the google-10000-english Github repository.

I additionally filtered these words down to only nouns, verbs, and adjectives, using the spacy part-of-speech tagger. This reduced the total number of good clue words from 10,000 to 7,830.

To find the clue that best matches the word cluster, I calculate the distance between all clues and all of the words in the cluster. Similar to the method used in the hierarchical clustering step, the average distance between the clue and all words in the cluster is used as the distance between the clue and the cluster.

I filter out clues that overlap with any words on the board. We can't only rely on matching whole strings, because words can take on different forms (e.g. "run", "runs", "running"). I use the NLTK PorterStemmer to stem the words to their base form for comparison. As an example, this would convert all three forms of "run": "run", "runs", "runner", to the stemmed form "run".

With overlapping clues filtered out, I take the top k closest clues as the best clues for that cluster.

Limitations and future ideas

Overall, the approach works OK, but could be improved. I find the word clusters to make sense, but the clues that best match clusters could be better. The clues generally match the sense of the cluster, and sometimes may even be considered clever, but the quality is inconsistent.

Here are some examples of good and bad clues, in the format (words → clues):

Good:

shoe leather → footwear boots clothing

forest rain ocean → tropical coastal waters

beach ocean island → shore waters coastal

fountain vase → sculpture marble porcelain

Bad:

horse lion zebra → elephant cat dog

doctor daughter boy → girl mother son

girl school → boys teacher parents

thailand sweden → denmark finland netherlands

Clue words that are closest to the meaning of words in a cluster will not always capture the general meaning of the cluster. For example, the cluster ["horse", "lion", "zebra"] has best clues ["elephant", "cat", "dog"]. All of these clues are animals, and animals are semantically close to one another, but they are too specific to be a helpful clue. A better clue would be "animal" or "quadruped", the specific word for a four-legged animal.

In the future, I am considering using more sophisticated language models, such as BERT, or a pretrained transformer, which can capture semantic and contextual relations between words better. In addition, I am also planning on investigating alternative words clustering approaches, such as mixture modeling, as this would allow for words to have membership in multiple clusters, instead of the strict hierarchical approach used here.